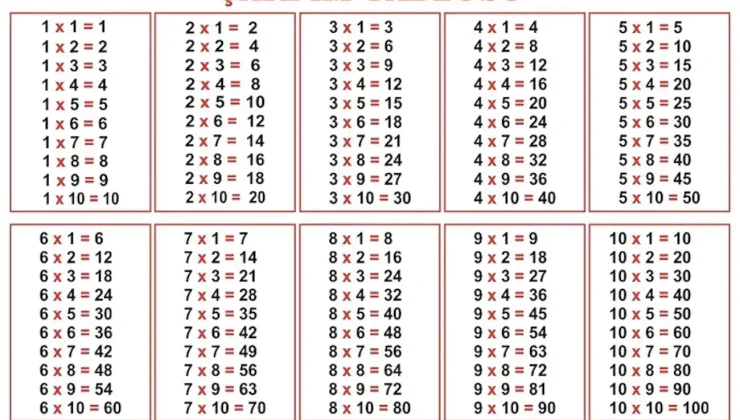
Çarpım tablosu pdf, matematiksel işlemlerde yaygın olarak kullanılan ve çarpma işleminin sonuçlarını düzenli bir şekilde sunan bir araçtır. Temel matematik becerilerini geliştirmek için öğrencilere öğretilen çarpım tablosu, matematiksel hesaplamaları hızlandırmada ve matematiksel kavramları anlamada büyük bir rol oynar. Bu makalede, çarpım tablosunun tanımını, kullanım alanlarını ve önemini keşfedeceğiz.

Çarpım Tablosunun Tanımı

Çarpım tablosu, çarpma işlemi sonucunda ortaya çıkan değerlerin düzenli bir şekilde sıralandığı bir tablodur. Tipik olarak, tablonun sol tarafında çarpanlar (genellikle 1’den 10’a kadar olan sayılar) yer alırken, üst tarafında çarpılanlar bulunur. Tablonun içindeki hücreler, çarpan ve çarpılan sayılarının çarpımının sonucunu gösterir. Örneğin, 3’ün 4 ile çarpımı 12 olduğu için, çarpım tablosunun 3. satırı ve 4. sütunu kesiştiği noktada 12 yazılıdır.

Çarpım Tablosunun Kullanım Alanları

Çarpım tablosu, temel matematiksel hesaplamaları yaparken sıklıkla kullanılır. İlköğretimde öğrencilere çarpma işlemini öğretmek ve matematik becerilerini geliştirmek için çarpım tablosu önemli bir araçtır. Özellikle büyük çarpımların hızlı bir şekilde bulunması gereken durumlarda çarpım tablosu kullanılır. Ayrıca, çarpım tablosu matematiksel problem çözme becerilerini geliştirmeye yardımcı olur ve ileri matematik konularıyla bağlantı kurmada temel bir yapı oluşturur.

Çarpım Tablosunun Önemi

Çarpım tablosu, matematik öğreniminde temel bir taş olarak kabul edilir. Öğrenciler, çarpım tablosunu öğrenerek çarpma işlemini daha kolay ve hızlı bir şekilde gerçekleştirebilirler. Bu, genel matematik becerilerini güçlendirir ve ileri matematik konularında daha başarılı olmalarını sağlar. Ayrıca, çarpım tablosunun öğrenilmesi, zihinsel hesaplama becerilerini geliştirir ve matematiksel düşünme yeteneklerini artırır.

Tarihi Gelişim

Çarpım tablosu, matematiksel hesaplamaların temel bir bileşeni olup binlerce yıl öncesine dayanan bir geçmişe sahiptir. İnsanlar, çoğu zaman çoğaltma işlemlerini kolaylaştırmak ve sonuçları hızlıca bulmak için düzenli bir tablo kullanma ihtiyacını fark etmişlerdir. Bu nedenle, çarpım tablosunun tarihi, insanların matematiksel hesaplamaları organize etme ve daha etkili bir şekilde gerçekleştirme çabalarına dayanmaktadır.

Çarpım tablosunun kökenleri, antik dönemlere kadar uzanır. Örneğin, Mısır’da yaşayan eski Mısırlılar, 2. binyılda çarpım tablosu benzeri bir yapıyı kullanmışlardır. Eski Mısırlılar, geometri ve inşaat projelerinde pratik hesaplamalar yapmak için bu tabloyu kullanıyorlardı. Benzer şekilde, Mezopotamya’da da çarpım tablolarının erken örneklerine rastlanmaktadır. Mezopotamyalılar, çarpma işlemini gerçekleştirmek için çeşitli metotlar kullanırken, bazı çarpım tabloları da geliştirmişlerdir.

Ancak, çarpım tablolarının daha yaygın ve sistemli bir şekilde kullanılmaya başlaması Ortaçağ döneminde gerçekleşti. İslam dünyası, bu dönemde matematik ve bilime büyük katkılarda bulunmuştur. 9. ve 10. yüzyıllarda İslam matematikçileri, Hint-Arap rakamlarının kullanımını yaygınlaştırmış ve çeşitli matematiksel eserler üretmişlerdir. Bu eserlerde, çarpım tabloları ve çarpma işlemiyle ilgili öğretiler bulunmaktadır. Özellikle Muhammed ibn Müsâ al-Hârizmî’nin “Hesaplamanın Temelleri Üzerine” adlı eseri, çarpım tablolarının sistematik bir şekilde sunulduğu ilk çalışmalardan biridir.

Ortaçağ Avrupa’sında da çarpım tablolarının kullanımı yaygınlaşmıştır. Özellikle matematik eğitimi alanında önemli bir figür olan Alman matematikçi Johannes Widmann, 15. yüzyılda “Arithmetic” adlı eserinde çarpım tablolarını ayrıntılı bir şekilde açıklamıştır. Widmann’ın eseri, Avrupa’da çarpım tablolarının popülerleşmesine ve matematik öğretiminde kullanılmasına büyük katkı sağlamıştır.

Günümüzde, çarpım tabloları hala temel matematik eğitiminin bir parçasıdır ve ileri matematiksel hesaplamalarda da kullanılmaktadır. Teknolojinin ilerlemesiyle birlikte, çarpım tabloları daha interaktif ve görsel bir şekilde sunulmaktadır. Mobil uygulamalar ve çevrimiçi araçlar, öğrencilere eğlenceli bir şekilde çarpım tablolarını öğrenme fırsatı sunmaktadır. Ancak, geçmişten günümüze kadar olan süreçte, çarpım tablolarının temel amacı değişmemiştir: matematiksel hesaplamaları daha düzenli ve etkili bir şekilde gerçekleştirmek.

Çarpım Tablosunun Yapısı

Çarpım tablosu, matematiksel hesaplamaları düzenli bir şekilde sunan ve çarpma işleminin sonuçlarını gösteren bir araçtır. Yapısı, belirli bir düzen ve format içinde oluşturulmuştur ve çarpanlarla çarpılanların çarpım sonuçlarını içeren hücrelerden oluşur. Bu makalede, çarpım tablosunun yapısını daha ayrıntılı bir şekilde inceleyeceğiz.

Çarpım tablosunun temel yapısı, bir sütun ve bir satır olmak üzere iki boyutlu bir düzlem üzerinde yer alır. Genellikle, tablonun sol tarafında çarpanlar, üst tarafında ise çarpılanlar bulunur. Çarpanlar sırasıyla 1’den 10’a kadar olan sayıları temsil ederken, çarpılanlar da aynı şekilde 1’den 10’a kadar olan sayılardır. Bu nedenle, tipik bir çarpım tablosu 10×10 boyutlarında bir tablo olarak düşünülebilir.

Çarpanlar ve çarpılanlar arasındaki kesişim noktaları, çarpma işleminin sonucunu gösteren hücrelerdir. Her hücre, bir çarpanın bir çarpılanla çarpımının sonucunu içerir. Örneğin, 3’ün 4 ile çarpımı 12 olduğunda, çarpım tablosunun 3. satırı ve 4. sütunu kesiştiği noktada 12 yazılıdır. Bu düzen, çarpanlar ve çarpılanlar arasındaki ilişkiyi net bir şekilde gösterir ve çarpım sonuçlarının kolayca bulunmasını sağlar.

Çarpım tablosu, genellikle düzenli bir şekilde sunulur. Sayılar genellikle düşey ve yatay olarak artan bir sırayla yerleştirilir. Örneğin, çarpanlar sırasıyla sol tarafta artan bir şekilde 1, 2, 3, …, 10 olarak yer alırken, çarpılanlar üst tarafta aynı şekilde artan bir sırayla 1, 2, 3, …, 10 olarak yerleştirilir. Bu düzen, tablonun okunmasını ve istenilen çarpım sonucunun hızlı bir şekilde bulunmasını kolaylaştırır.

Çarpım tablosunda bazı hücreler özel bir şekilde düzenlenebilir. Genellikle, tablonun köşesinde yer alan hücrede, iki sayının çarpımının sonucunu gösteren sayı yerine çarpan ve çarpılan sayıları çarpan işaretiyle (x veya ) ayrılarak yazılabilir. Örneğin, çarpım tablosunun sol üst köşesinde yer alan hücrede, x veya * sembolüyle ayrılarak 1×1 veya 11 şeklinde yazılabilir.

Çarpım Tablosunun Yararları

Çarpım tablosu, matematiksel hesaplamaları daha kolay ve hızlı bir şekilde gerçekleştirmemizi sağlayan temel bir araçtır. Özellikle çarpma işlemine dayalı problemleri çözerken ve matematiksel becerilerimizi geliştirirken büyük faydalar sağlar. Bu makalede, çarpım tablosunun yararlarını daha ayrıntılı bir şekilde inceleyeceğiz.

1. Hızlı ve Doğru Hesaplama: Çarpım tablosu, çarpanlar ve çarpılanlar arasındaki ilişkiyi sistemli bir şekilde sunar. Bu düzen, çarpma işlemi sonuçlarını hızlı ve doğru bir şekilde bulmamızı sağlar. Örneğin, bir çarpanı 6 olan bir sayıyı başka bir sayıyla çarpmamız gerektiğinde, çarpım tablosunu kullanarak sonucu hemen bulabiliriz.
2. Matematiksel Becerilerin Geliştirilmesi: Çarpım tablosu, öğrencilerin matematik becerilerini geliştirmelerine yardımcı olur. Çarpma işlemini ve matematiksel ilişkileri anlamak için öğrencilere çarpım tablosuyla çalışma fırsatı verilir. Bu, öğrencilerin sayılar arasındaki çarpma ilişkilerini görsel bir şekilde anlamalarını sağlar ve matematiksel düşünme yeteneklerini geliştirir.
3. Hafıza ve Zihinsel Hesaplama Yeteneklerinin Güçlenmesi: Çarpım tablosunu ezberlemek, öğrencilerin hafızalarını güçlendirir. Çarpım tablosundaki sayıları hatırlama ve çarpma işlemlerini zihinsel olarak gerçekleştirme becerisi, öğrencilerin zihinsel hesaplama yeteneklerini geliştirir. Bu, daha karmaşık matematik problemlerini hızlı bir şekilde çözmelerine yardımcı olur.
4. Matematiksel İlişkilerin ve Desenlerin Keşfedilmesi: Çarpım tablosu, matematiksel ilişkileri ve desenleri keşfetmek için bir temel oluşturur. Öğrenciler, tabloda belirli desenlerin ortaya çıktığını fark edebilirler. Örneğin, her satırdaki sayıların 1’den başlayarak arttığını veya her sütundaki sayıların belirli bir çarpanla çarpıldığını gözlemleyebilirler. Bu, matematiksel desenleri ve ilişkileri keşfetme becerilerini geliştirir ve ileri matematik konularına geçerken avantaj sağlar.
5. Çoklu Konseptlerin Öğrenimi: Çarpım tablosu, çarpanlar ve çarpılanlar arasındaki ilişkileri anlamamızı sağladığı gibi, çeşitli matematiksel kavramları da içerir. Çarpanların artışı, çarpma işlemine dayalı bölme kavramını ve tersi ilişkiyi anlamamıza yardımcı olur. Aynı zamanda, çarpım tablosuyla çalışmak, sayıların toplama ve çıkarma işlemleriyle olan ilişkilerini de keşfetmemizi sağlar.

Çarpım tablosu matematik eğitiminin temel bir unsuru olup hızlı ve doğru hesaplama, matematiksel becerilerin geliştirilmesi, hafıza ve zihinsel hesaplama yeteneklerinin güçlenmesi, matematiksel ilişkilerin ve desenlerin keşfedilmesi, ve çoklu matematik kavramlarının öğrenimi gibi birçok yarar sağlar. Çarpım tablosunun öğrenimi, matematiksel anlayışımızı derinleştirir ve matematikle ilgili konulara daha güvenli bir şekilde ilerlememizi sağlar.

Çarpım Tablosunun Pratik Kullanımı

Çarpım tablosu, matematiksel hesaplamaların hızlı ve etkili bir şekilde yapılmasını sağlayan temel bir araçtır. Ancak, çarpım tablosunun yalnızca matematik derslerindeki bir öğe olmadığını unutmamak önemlidir. Gerçek hayatta da çeşitli pratik durumlarda çarpım tablosu kullanılabilir ve faydaları oldukça büyük olabilir. Bu makalede, çarpım tablosunun pratik kullanımını daha ayrıntılı bir şekilde inceleyeceğiz.

1. Hızlı Satın Alma Hesaplamaları: Günlük hayatta, alışveriş yaparken çarpım tablosunu kullanmak oldukça faydalı olabilir. Örneğin, markette fiyatı 5 TL olan bir ürünü 7 adet almak istediğimizi düşünelim. Toplam tutarı hızlıca hesaplamak için 5 ile 7’nin çarpım sonucunu çarpım tablosundan hemen bulabiliriz. Böylece, toplam maliyeti kolayca öğrenebiliriz.
2. Yemek Tariflerinde Ölçü Birimleri: Yemek tariflerinde doğru ölçü birimlerini kullanmak önemlidir. Özellikle tariflerde malzemelerin belirli oranlarda çarpılması gerekebilir. Çarpım tablosu, örneğin tarifte belirtilen malzemeyi çeşitli katlarıyla çarpmak için kullanılabilir. Böylece, doğru miktarları elde edebilir ve yemekleri başarıyla hazırlayabiliriz.
3. Zaman ve Hız Hesaplamaları: Seyahat ederken veya zamanla ilgili herhangi bir durumu hesaplarken, çarpım tablosu bize yardımcı olabilir. Örneğin, bir aracın belirli bir hızla giderken belirli bir mesafeyi ne kadar sürede kat edeceğini hesaplamak istediğimizde, hızı kilometre/saat cinsinden çarpan ve mesafeyi kilometre cinsinden çarpılan olarak kullanabiliriz. Çarpım tablosu sayesinde, varış zamanını hızlıca tahmin edebiliriz.
4. Maliyet ve Bütçe Planlaması: Finansal planlama ve bütçe oluşturma süreçlerinde çarpım tablosu kullanmak oldukça yararlıdır. Örneğin, bir projenin maliyetini belirlemek veya bir gelir-gider tablosu hazırlamak için çeşitli faktörleri çarpmamız gerekebilir. Çarpım tablosu, bu tür hesaplamaları daha hızlı ve daha doğru bir şekilde yapmamıza yardımcı olur.
5. Ebat ve Ölçüm Hesaplamaları: İnşaat, mobilya montajı veya herhangi bir fiziksel projede çalışırken, çarpım tablosu boyut ve ölçüm hesaplamalarında kullanılabilir. Örneğin, bir duvarın uzunluğunu belirli bir oranda çarpmak veya bir alanın genişliğini ve yüksekliğini çarparak toplam alanı bulmak için çarpım tablosu kullanabiliriz. Bu, projeleri daha etkili bir şekilde planlamamızı sağlar.

Çarpım tablosunun pratik kullanımı, günlük hayatta karşılaştığımız birçok durumda bize yardımcı olabilir. Hızlı hesaplamalar, ölçüm birimleri, zaman tahminleri, maliyet hesaplamaları ve projelerin planlanması gibi alanlarda çarpım tablosu büyük bir avantaj sağlar. Bu nedenle, çarpım tablosunu yalnızca matematik derslerinde değil, pratik yaşamın bir parçası olarak da görmek önemlidir.

Çarpım Tablosunun Zeka Gelişimine Etkisi

Çarpım tablosu, matematiksel hesaplamaları yaparken kullanılan temel bir araç olarak bilinir. Ancak çarpım tablosunun sadece matematik öğrenimiyle sınırlı kalmadığını bilmek önemlidir. Aslında, çarpım tablosu zeka gelişimi üzerinde olumlu bir etkiye sahip olabilir. Bu makalede, çarpım tablosunun zeka gelişimi üzerindeki etkilerini daha ayrıntılı bir şekilde ele alacağız.

1. Matematiksel Mantığı Geliştirir: Çarpım tablosu, matematiksel ilişkileri ve desenleri anlamak için bir temel oluşturur. Öğrenciler, tablodaki sayıların nasıl bir düzene sahip olduğunu gözlemleyerek matematiksel mantığı geliştirir. Bu, sayılar arasındaki çarpma ilişkilerini anlamalarına ve matematiksel düşünme becerilerini güçlendirmelerine yardımcı olur.
2. Bellek Kapasitesini Artırır: Çarpım tablosunu ezberlemek, öğrencilerin bellek kapasitelerini artırır. Tabloyu tamamen öğrenmek, sayıları hatırlama ve çarpma işlemlerini hızlı bir şekilde gerçekleştirme becerisi kazandırır. Bu, beyin fonksiyonlarını aktive eder ve bellek yeteneklerini geliştirir.
3. Mental Hesaplama Becerisini Geliştirir: Çarpım tablosuyla çalışmak, öğrencilerin zihinsel hesaplama becerilerini güçlendirir. Çarpanlar ve çarpılanlar arasındaki ilişkiyi anlama, zihinsel olarak çarpma işlemi yapma ve sonuçları hızlıca hesaplama yetenekleri gelişir. Bu da genel olarak matematiksel problem çözme becerilerini iyileştirir.
4. Analitik Düşünmeyi Teşvik Eder: Çarpım tablosunu kullanırken, öğrenciler analitik düşünme becerilerini geliştirir. Sayılar arasındaki ilişkileri anlamak, örüntüleri gözlemlemek ve çeşitli stratejiler geliştirmek için analitik düşünmeyi kullanırlar. Bu, problem çözme yeteneklerini güçlendirir ve analitik düşünme becerilerini diğer alanlara da taşır.
5. Mantıksal Akıl Yürütme Yeteneğini Artırır: Çarpım tablosu, öğrencilerin mantıksal akıl yürütme yeteneklerini geliştirmelerine yardımcı olur. Çarpanları ve çarpılanları kullanarak sonuçları tahmin etme, doğrulama ve çıkarımlar yapma becerisi kazanırlar. Bu, matematiksel problemleri çözerken mantıksal bir yaklaşım geliştirmelerine katkı sağlar.
6. Desen ve Simetri Algısını İyileştirir: Çarpım tablosu, sayılar arasındaki desenleri ve simetriyi fark etmeyi teşvik eder. Öğrenciler, tablodaki düzeni gözlemleyerek desenler ve simetrik ilişkileri tanıma becerisi kazanır. Bu, matematiksel ve geometrik kavramları anlamalarına yardımcı olur.

Çarpım tablosu zeka gelişimine olumlu katkılarda bulunur. Matematiksel mantığı geliştirir, bellek kapasitesini artırır, mental hesaplama becerilerini güçlendirir, analitik düşünmeyi teşvik eder, mantıksal akıl yürütme yeteneğini artırır ve desen ile simetri algısını iyileştirir. Bu nedenle, çarpım tablosunun öğrenimi, öğrencilerin matematiksel yeteneklerini ve genel zeka seviyelerini geliştirmelerine yardımcı olur.

Çarpım Tablosunun Öğrenme Motivasyonuna Etkisi

Matematik öğrenimi, bazı öğrenciler için zorlu ve sıkıcı bir süreç olabilir. Ancak, çarpım tablosunun öğrenme sürecine dahil edilmesi, öğrencilerin motivasyonunu artırabilir. Çarpım tablosunun öğrenme motivasyonuna etkisi, matematik derslerindeki ilgiyi artırabilir ve öğrencilerin matematik becerilerini geliştirmelerine yardımcı olabilir. Bu makalede, çarpım tablosunun öğrenme motivasyonuna etkisini daha ayrıntılı bir şekilde ele alacağız.

1. Anlamlı ve Uygulanabilir Bağlantılar Kurar: Çarpım tablosu, gerçek dünya uygulamalarında kullanılan çarpma işlemlerine anlamlı bir bağlantı sağlar. Öğrenciler, günlük yaşamlarında gerçekleştirdikleri aktivitelerde çarpma işlemini kullanmanın önemini görebilirler. Örneğin, alışverişte fiyatları çarpmak veya yemek tariflerinde ölçü birimlerini çarpmak gibi durumlarla karşılaşırlar. Bu bağlantılar, matematik öğrenimini gerçek yaşamla ilişkilendirmeye yardımcı olur ve öğrencilerin öğrenme motivasyonunu artırır.
2. Hızlı ve Doğru Hesaplama Becerilerini Geliştirir: Çarpım tablosu, matematiksel hesaplamaları hızlı ve doğru bir şekilde yapma becerisini geliştirir. Öğrenciler, tabloyu ezberleyerek çarpma işlemlerini daha hızlı bir şekilde gerçekleştirebilirler. Bu, öğrencilerin matematik derslerinde daha fazla özgüven kazanmalarını sağlar. Hızlı ve doğru hesaplama yeteneği, öğrencilerin matematik problemlerini daha kolay çözmelerini sağlar ve başarı duygusunu artırır.
3. Görsel Öğelerle Etkileşimi Artırır: Çarpım tablosu, görsel öğelerle zenginleştirilmiş bir matematik aracıdır. Renkli ve düzenli bir tablo, öğrencilerin görsel olarak etkileşim kurmalarına yardımcı olur. Görsel öğeler, öğrencilerin tabloyu daha iyi anlamalarını ve hatırlamalarını sağlar. Bu, öğrencilerin matematiksel kavramları daha kolay algılamalarına ve öğrenmeye teşvik eder.
4. Oyun ve Rekabet Unsurlarıyla Motivasyonu Artırır: Çarpım tablosu öğrenme sürecine oyun ve rekabet unsurları eklemek, öğrencilerin motivasyonunu artırır. Örneğin, öğretmenler çarpım tablosu yarışmaları düzenleyebilir veya öğrenciler arasında küçük grup oyunları oynatabilir. Bu, öğrencilerin birbirleriyle etkileşimde bulunmasını sağlar ve matematik öğrenimini daha eğlenceli hale getirir. Oyun ve rekabet, öğrencilerin daha fazla ilgi göstermelerini ve aktif bir şekilde katılmalarını teşvik eder.
5. Bağımsızlık ve Özgüveni Artırır: Çarpım tablosunun öğrenimi, öğrencilere bağımsızlık kazandırır ve özgüvenlerini artırır. Öğrenciler, tabloyu ezberleyerek çarpma işlemlerini kendi başlarına yapabilme becerisi kazanır. Bu, matematik derslerinde daha bağımsız bir şekilde çalışmalarını sağlar ve özgüvenlerini artırır. Öğrenciler, başarıya ulaştıkça özgüvenlerini daha da güçlendirir ve matematik öğrenimiyle ilgili daha pozitif bir tutum geliştirir.

Çarpım tablosunun öğrenme motivasyonuna olumlu bir etkisi vardır. Anlamlı bağlantılar kurar, hızlı ve doğru hesaplama becerilerini geliştirir, görsel öğelerle etkileşimi artırır, oyun ve rekabet unsurlarıyla motivasyonu artırır ve bağımsızlık ile özgüveni güçlendirir. Öğrencilerin matematik öğrenimine olan ilgisini artırarak, matematik becerilerini geliştirmelerine ve başarıyı yakalamalarına yardımcı olur.

Çarpım Tablosu PDF (Tıkla ve İndir)

Aşağıda bulunan PDF görüntüsünde sağ üst tarafta bulunan yazıcı ya da aşağı ok tuşlarına basarsanız indirebilir ve yazdırabilirsiniz. Çarpım Tablosu PDF içeriğimizin burada sonuna geldik bir sonraki içeriğimizde görüşmek üzere kendinize iyi bakın…